Notation and naming

Time, time interval, time scale

A time is noted with a t, a time interval with dt,δt, Δt and as τ in process parameters. The distinction should be clear between a time (or an epoch), like in ”today at 1 o’clock”, and a time interval, like in ”1 hour ago”. A time interval is a fairly abstract concept, measured essentially by the beats of a pendulum. The ratio of 2 time intervals gives a real number. For example, for a time interval dt of 1 week, the ratio dt ∕ 1h = 168 (a real number), where 1h is a time interval of 1 hour. Such ratios appear in exponential moving average (EMA), or in process definitions, in the form dt ∕ τ, with τ a characteristic time interval of the process. In finance, it is usual to ’annualize’ volatility. This is done by multiplying with the factor ∘ ------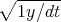
1y∕dt , where 1y denotes a 1 year time interval.

Time and time intervals are measured on a given time scale. Usually, this is the physical time scale, as assumed in the discussion in the previous paragraph. In finance, other time scales can be more appropriate, like a business time scale, or a transaction time scale. The deseasonalization of the empirical data is done using a continuous version of the business time scale (which contains 5 days per week of daily data). We use the words ’time scale’ for a scale to measure times and time intervals, and the words ’time interval’ or ’time horizon’ for time differences.

Notation for time series

A time series is denoted by a single letter, like r for the price change (or return) time series.
The value of a time series at a given time is denoted with parenthesis, like r(t) for the return at a given time t.
The parameter(s) of a time series are denoted between square bracket [⋅], like r[dt] for the return time series, with the returns computed over a given time interval dt. The return at a given time t and for a given time interval dt is noted r[dt](t).

Historical, realized and centered

A quantity computed using data up to t is called historical. For example c $rhistorical[dt](t) = p(t) - p(t - dt)$
is the historical return (beware that our definition of the return is different by the normalization from this simple example).
A quantity computed using data in the future of t is called realized. For example $rrealized[dt](t) = p(t + dt) - p(t)$
is the realized return.
This is a standard convention in time series forecasting: a forecast is constructed using historical values, and the forecasts are compared to the realized values.
Some quantities are computed around t, and are called centered. They use information in the past and future of t. For example the centered price change can be defined as $r0[dt](t) = p(t + dt∕2) - p(t - dt∕2),$
and measure the price change occurring around t over a time horizon dt. In the empirical analysis, the centered volatility change is studied in relation with historical quantities, as this gives a dynamic measure of the volatility behaviors.
In formulas and axes, historical, realized and centered quantities are denoted respectively with the indices h, r and 0.