Base information Home Purpose FAQ Notations Formula Figure descriptions Indexes Links to time series Pop-up to time series Two-time series comparison One figure comparison

GARCH(1,1) process with relative returns

With relative returns, the price update equation takes the form

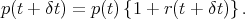(1)

This form is consistent with using a relative return definition

(2)

When analyzing historical time series, logarithmic returns or relative returns can be used. The choice for the definition is essentially a mater of taste, with differences mainly in the skewness of the resulting return distribution.

When defining a process, the returns are generated with a formula akin to r = σϵ, where the innovations ϵ are drawn from a given distribution. But the subsequent update equation for the price is ill defined when the innovations have a fat-tail distribution (see e.g. O’Neil and Zumbach [2009]).

With logarithmic returns, the next price is given by p(t + δt) = p(t) exp(σϵ). Given the price p(t), the expectation of the next price leads to a diverging integral when the distribution for ϵ decays as a power law (because the exponential term in ϵ grows faster than any power law).

With relative returns, the same expectation for p(t + δt) is well defined provided that the distribution for ϵ decays faster than 1∕ϵ². Because reproducing empirical data requires to have fat-tailed innovations, relative returns should be used in order to have well defined mathematical properties.

For the GARCH(1,1) process with relative return, the volatility part is identical to the GARCH(1,1) process.

The parameters for the simulations are identical to the GARCH(1,1) with logarithmic returns

• σ∞ = 0.11
• w∞ = 0.10
• τ = 1 day

The innovations have a Student distribution with 3.3 degree of freedom. The simulation time corresponds to 200 years with a time increment δt = 3 minutes.

References